Arcos y Círculos
Para definir Arcos
Al definir arcos para un símbolo, como los arcos en un transformador o derivación, tenga en cuenta el siguiente diagrama. La siguiente figura muestra un cuadrado formado por cuatro cuadrantes. 0 ° se muestra a la derecha. El movimiento del arco procede en sentido horario desde ese punto. En la figura, el arco se define con un ángulo inicial de 0 ° y un ángulo de barrido de 180 °.
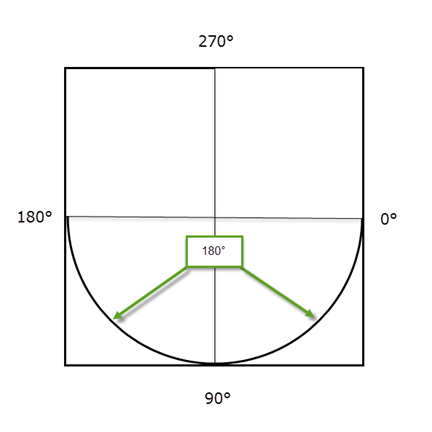
Figura 1: Arco a Partir de 0 ° con un Ángulo de Barrido de 180 °
En la figura siguiente, el arco se define con un ángulo de inicio de 270 ° y un ángulo de barrido de 180 °.
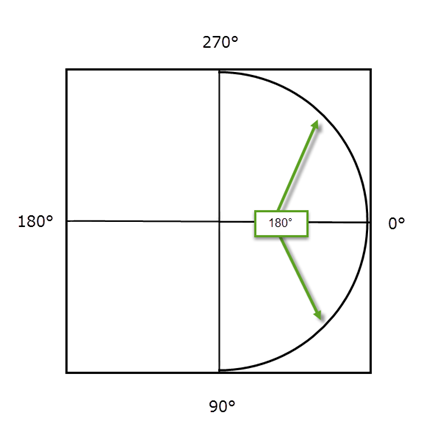
Figura 2: Arco Desde 270 ° con un Barrido de 180 °
En ambos casos, el ángulo de barrido es de 180 °, creando un semicírculo. La diferencia está en el punto de partida.
Arcos Elípticos
Los ejemplos anteriores muestran un arco circular. Como la altura y el ancho no se especifican, se supone que son idénticos, entonces el resultado es un círculo (aunque sólo una parte del círculo se muestra en función del punto de inicio y el ángulo de barrido que se ha definido).
También puede crear un arco elíptico estableciendo parámetros de anchura y altura. Utilice esto para aplanar el arco. El ejemplo siguiente se toma de la plantilla de símbolos para definir un condensador ANSI de barra inferior.

Figura 3: Símbolo de Condensador ANSI
<SymbolTemplate> (PlantillaSímbolo)
<Line X1="10" Y1="0" X2="10" Y2="9" />
<Line X1="5" Y1="9" X2="15" Y2="9" />
<Line X1="10" Y1="12" X2="10" Y2="20" />
<Arc Left="2" Top="12" Width="16" Height="6" StartAngle="205" SweepAngle="130" />
</SymbolTemplate> (Fin PlantillaSímbolo)
Los tres primeros valores de "Line" definen las líneas rectas en el símbolo. El último conjunto de valores "Arc" define la línea curva en el símbolo. El ejemplo siguiente muestra todo el círculo elíptico que crea la curva, pero sólo la porción entre las líneas de puntos verdes (definidas por los ángulos de inicio y de barrido) se muestran en el símbolo final. El área amarilla resaltada indica la anchura (12 puntos de la cuadrícula) y la altura (6 puntos de la cuadrícula) que determinan la forma total de la elipse.
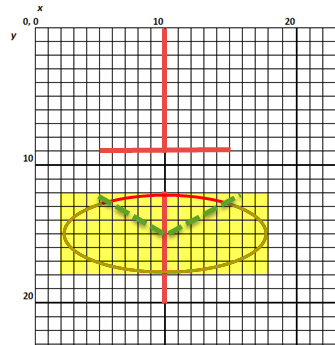
Figura 4: Ejemplo de Arco Elíptico
Para Definir Círculos
Los círculos parecen similares a los arcos pero se definen de manera diferente. Para un círculo, es necesario definir las coordenadas X y Y y para especificar un radio. Todos se especifican en puntos de cuadrícula. Por ejemplo, en ANSI, para un motor de inducción CA, se utiliza la siguiente información:
<SymbolTemplate> (PlantillaSímbolo)
<Circle X="8" Y="8" Radius="8" FillStyle="None"/>
<Polyline Points="5 11, 5 5, 8 10, 11 5, 11 11"/>
</SymbolTemplate> (Fin PlantillaSímbolo)
Las coordenadas X y Y determinan el centro del círculo. El radio se origina desde el centro del círculo. Esto significa que el centro del círculo está en las coordenadas 8,8, y hay 8 puntos de la cuadrícula en cada lado del centro al borde del círculo.
En una cuadrícula, que se vería así:
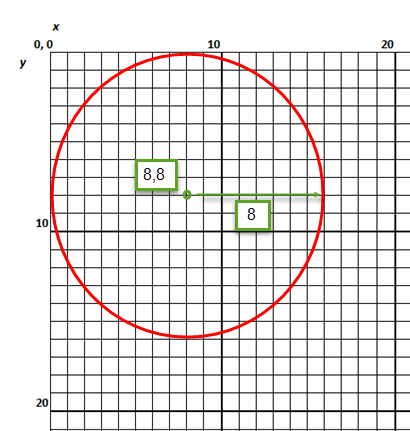
Figura 5: Definición de un Círculo para un Símbolo de Motor
Nota: Los puntos de polilínea se describen en un tema aparte. Ver Polilíneas.
Más Información
| Para Personalizar Símbolos de Diagrama-unifilar | Polilíneas |
| Etiquetas Definiciones de Símbolo | Polígonos |
| Coordinadas | Texto |
| Rectángulos y Líneas | Curvas Bezier |
